Генетические алгоритмы

Генетический алгоримтм является основным в группе так называемых эволюционных алгоритмов. Основоположником его принято считать Дж. Холланда.[12]. Однако для начального ознакомления можно порекомендовать более поздние и популярные источники [13] .

Ссылаясь на свободную энциклопедию «Википедия», определим ГА следующим образом:

«Генетический алгоритм (англ. genetic algorith) - это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию». Комбинирование и вариация искомых параметров достигаются путем применения в цикле алгоритма известных даже из школьного курса биологии генетических операторов - кроссинговера («скрещивания»), мутации и инверсии. Схематично алгоритм можно представить следующим образом (Рис.1.7.)

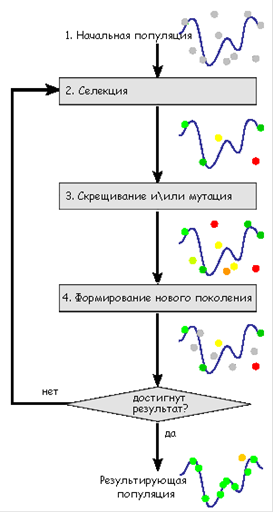
Рис.1.7. Схема генетического алгоритма.

Постановка задачи генетического алгоритма формально звучит очень просто - это нахождение минимума (желательно глобального) для многомерной функции

F(x1,x2, . . ., xn).

Эту функцию в контексте генетического алгоритма называют функцией приспособленности (fitness function), а конкретный вектор-параметр, для которого она вычисляется - особью. Точнее говоря, особь в классическом генетическом алгоритме представлена своей «хромосомой» - бинарным представлением, кодирующим вещественные компоненты вектора, характеризующего особь. Вещественное представление особи еще называют фенотипом, а бинарное - генотипом. Генетический алгоритм должен осуществлять как процесс кодирования фенотипа в генотип, так и обратное декодирование.

. В генетическом алгоритме в начале генерируется начальная популяция - множество особей (их хромосом). Первоначально значения параметров фенотипа - произвольные случайные величины в допустимом диапазоне изменения.

. На фазе селекции в популяции выбираются две особи для дальнейшего размножения путем скрещивания. При выборе двух особей генетический алгоритм отдает предпочтение особям с большим значением функции приспособленности, однако делает он это не строго детерминировано, а вероятностно. Для выбора часто принято использовать достаточно известный «метод рулетки», при котором вероятность остановки рулетки на некотором секторе пропорциональна его площади (или угловой мере).

. На третьей фазе к выбранной паре применяют операцию скрещивания (кроссовер), которая схематично выглядит следующим образом (Рис.1.8.):

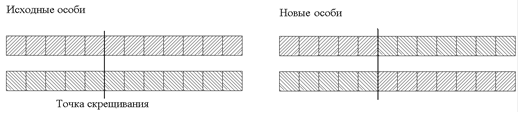
Рис.1.8. Схема кроссовера.

Далее во многих модификациях из двух новых особей остается одна - с наилучшей функцией приспособленности. Оставшаяся хромосома с заданной вероятностью может быть дополнительно подвергнута операции мутации и инверсии.

Оператор мутации изменяет значение случайно выбранного гена в хромосоме на противоположное (т.е. с 1 на 0 или наоборот).

Оператор инверсии изменяет значение всех генов в хромосоме на противоположное (т.е. с 1 на 0 или наоборот).

. Стадия формирования нового поколения. Здесь нужно удалить одну особь из популяции, чтобы сохранить постоянной величину популяции. И в этом случае следует обратить внимание на одну особенность. Считается что удаление должно отдавать предпочтение наихудшим особям. Однако достаточно эффективный метод рулетки здесь не подходит. В литературе часто предлагают использовать турнирный метод. Это напоминает соревнования по олимпийской системе, когда в каждом туре из двух команд-соперниц остается только победитель. Однако такой подход довольно трудоемкий при большом размере популяции.

В данной работе используется другой подход, который кажется интуитивно правильным, хотя в литературе не найдены сведения о его использовании.

. Возможны различные условия остановки алгоритма: истечение заданного количества шагов эволюции, стабилизация интегральной для популяции величины приспособленности и их комбинация.

В конце концов, после завершения цикла алгоритма возникает популяция с достаточно высокой функцией приспособленности ее особей. Наилучшая особь в популяции может считаться решением задачи.